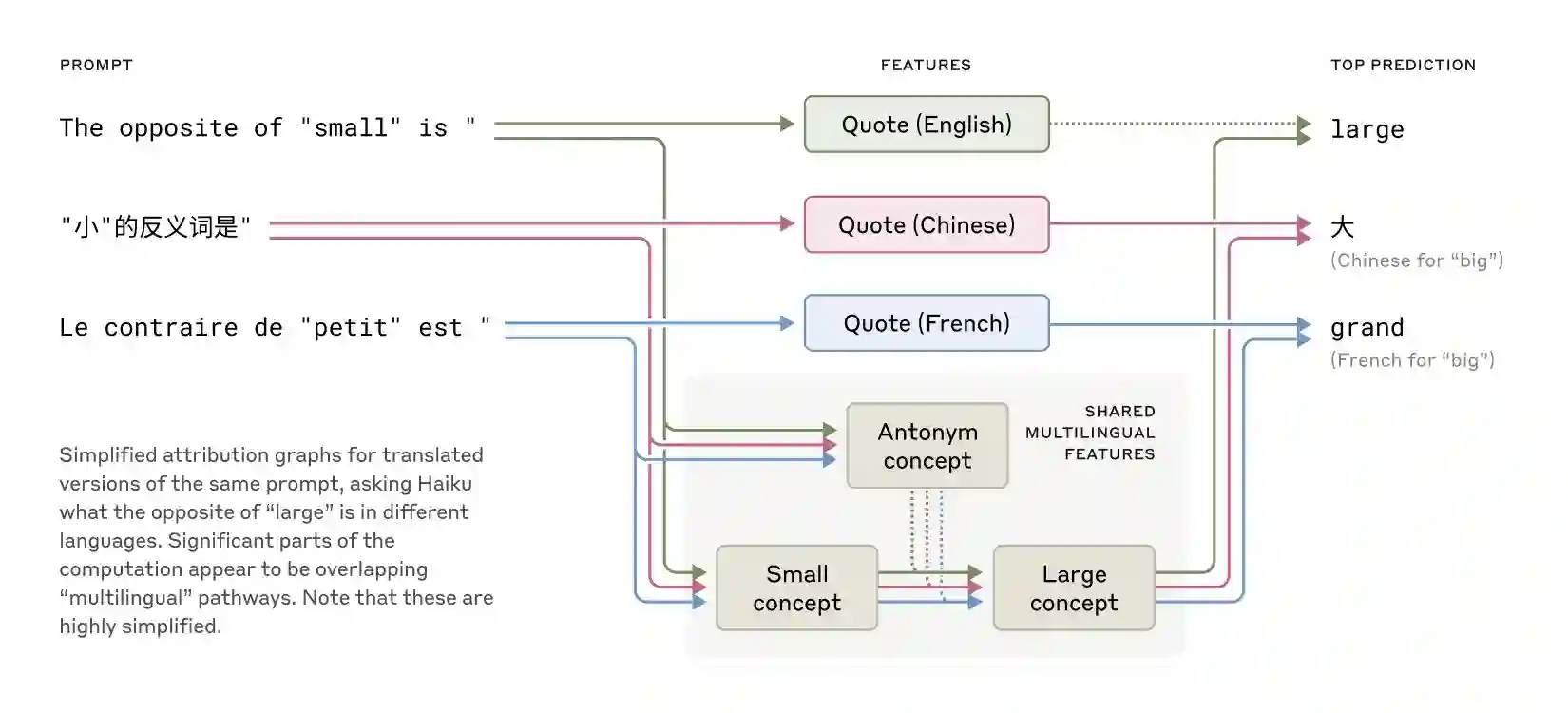
How Claude Does Math

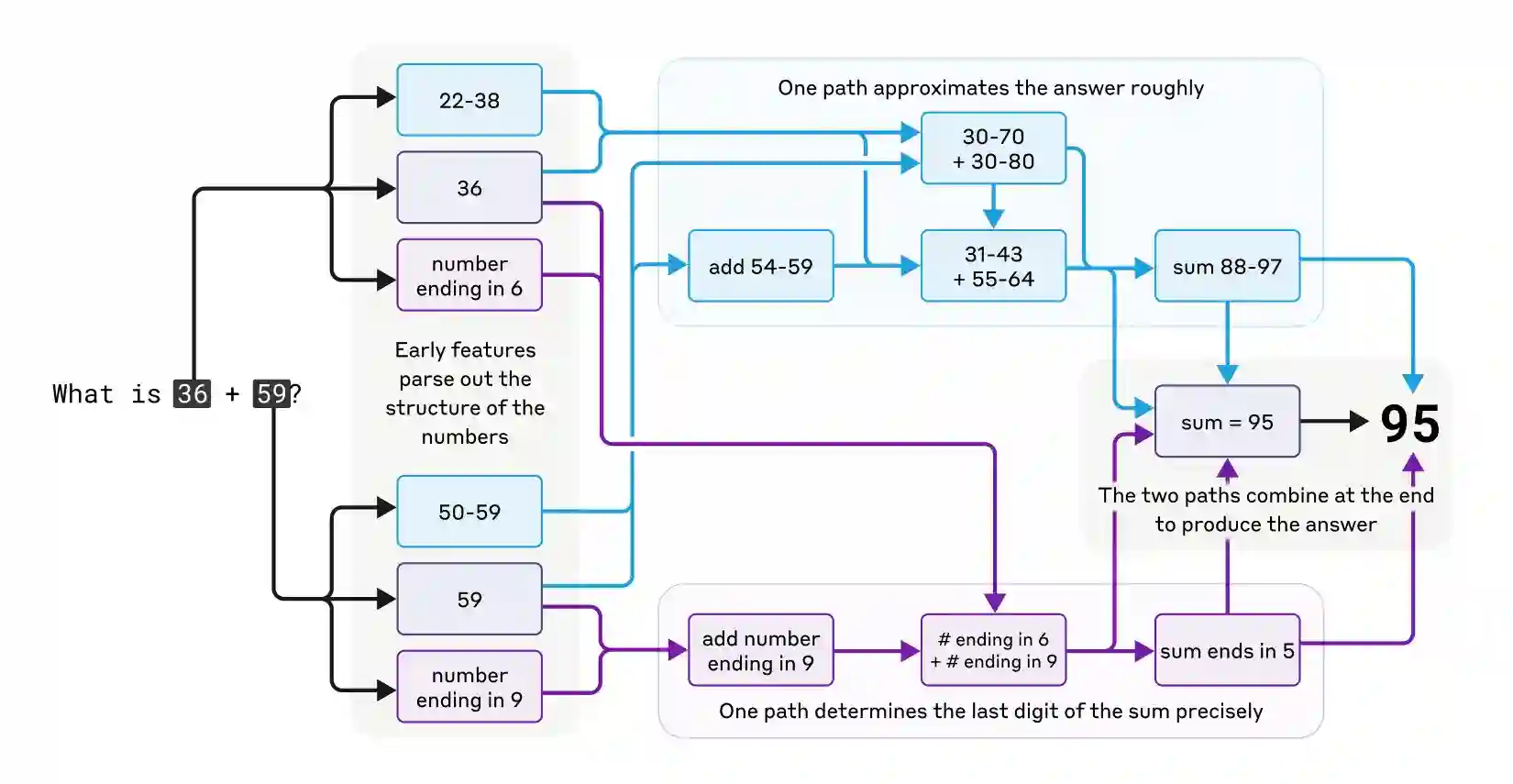
Claude was not designed as a calculator; it was trained on text and does not have mathematical algorithms. However, it can correctly add numbers "in its head." How does a system trained to predict the next word in a sequence calculate, for example, 36+59, without writing out each step?

One possible explanation is that the model may have memorized large addition tables and simply outputs the answer to any given sum because that answer is in its training data. Another possibility is that it follows traditional addition algorithms that we learn in school. Instead, we find that Claude employs multiple computational paths that work in parallel. One path computes a rough approximation of the answer, while the other focuses on precisely determining the last digit of the sum. These paths interact and combine with one another to produce the final answer. Addition is a simple behavior, but understanding how it works at this level of detail, involving a mix of approximate and precise strategies, might teach us something about how Claude tackles more complex problems.

I will explain the flowchart that shows how Claude performs the addition of 36 + 59. The diagram illustrates that Claude uses parallel computational paths to solve this addition problem:

The upper path (in blue) approximates the answer roughly: - It recognizes 36 is in the range 22-38 - It recognizes 59 is in the range 50-59 - These ranges lead to approximate sums: 30-70 + 30-80 - It calculates more precise ranges: 31-43 + 55-64 - This leads to a sum range of 88-97

The lower path (in purple) determines the exact last digit: - It identifies 36 as "number ending in 6" - It identifies 59 as "number ending in 9" - When adding numbers ending in 6 and 9, the result ends in 5 - This precisely determines the last digit

The two paths converge to produce the final answer: - The approximate range (88-97) combined with knowing the last digit (5) - Both paths confirm the answer is 95

The diagram shows that Claude does not simply memorize addition tables or follow traditional algorithms. Instead, it uses a combination of approximation strategies and precise digit calculations working in parallel to arrive at the correct answer of 95. This approach suggests that Claude's problem-solving abilities might involve similar parallel processing for other more complex tasks, using both approximate and precise computational paths that work together.