Come Claude fa i calcoli
Claude, non progettato come calcolatrice, somma correttamente usando percorsi computazionali paralleli. Un percorso approssima la somma, l'altro determina l'ultima cifra. Questo metodo suggerisce capacità di problem-solving simili per compiti complessi.
Claude non è stato progettato come una calcolatrice; è stato addestrato su testi e non dispone di algoritmi matematici. Tuttavia, riesce a sommare numeri correttamente "nella sua testa". Come fa un sistema addestrato a prevedere la parola successiva in una sequenza a calcolare, ad esempio, 36+59, senza scrivere ogni passaggio?
Una possibile spiegazione è che il modello abbia memorizzato enormi tabelle di addizione e semplicemente restituisca la risposta a qualsiasi somma perché essa è presente nei dati di addestramento. Un'altra possibilità è che segua gli algoritmi di addizione tradizionali che apprendiamo a scuola. Invece, scopriamo che Claude utilizza più percorsi computazionali che lavorano in parallelo. Un percorso calcola un'approssimazione grossolana della risposta, mentre l'altro si concentra sulla determinazione precisa dell'ultima cifra della somma. Questi percorsi interagiscono e si combinano per produrre la risposta finale. L'addizione è un comportamento semplice, ma comprendere come funziona a questo livello di dettaglio, coinvolgendo una combinazione di strategie approssimative e precise, potrebbe insegnarci qualcosa su come Claude affronta problemi più complessi.
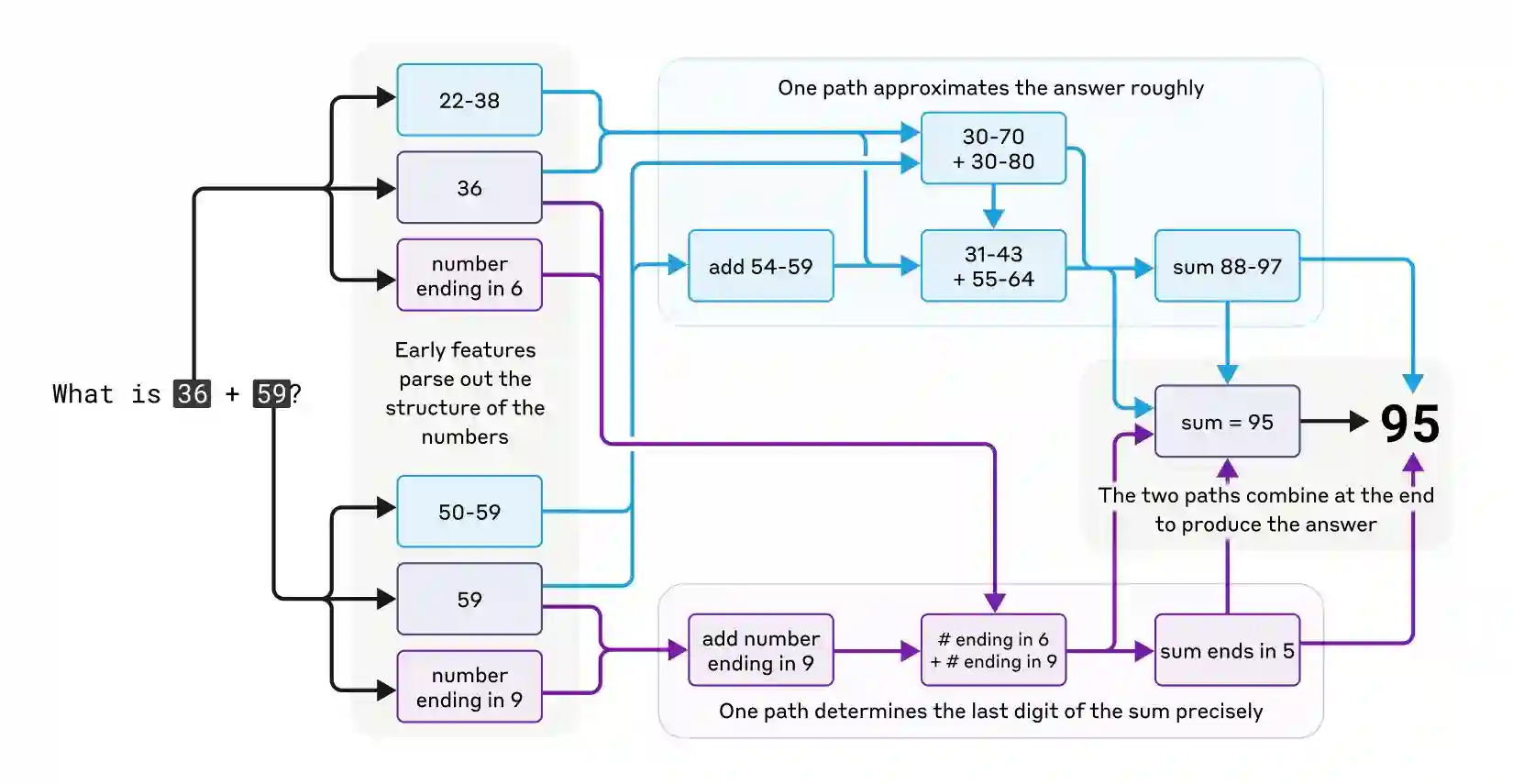
Spiegherò il diagramma che mostra come Claude esegue l'addizione di 36 + 59. Il diagramma illustra che Claude utilizza percorsi computazionali paralleli per risolvere questo problema di addizione:
Il percorso superiore (in blu) approssima grossolanamente la risposta: - Riconosce che 36 è nell'intervallo 22-38 - Riconosce che 59 è nell'intervallo 50-59 - Questi intervalli portano a somme approssimative: 30-70 + 30-80 - Calcola intervalli più precisi: 31-43 + 55-64 - Questo porta a un intervallo di somma di 88-97
Il percorso inferiore (in viola) determina l'ultima cifra esatta: - Identifica 36 come "numero che termina in 6" - Identifica 59 come "numero che termina in 9" - Quando si sommano numeri che terminano in 6 e 9, il risultato termina in 5 - Questo determina precisamente l'ultima cifra
I due percorsi convergono per produrre la risposta finale: - L'intervallo approssimativo (88-97) combinato con la conoscenza dell'ultima cifra (5) - Entrambi i percorsi confermano che la risposta è 95
Il diagramma mostra che Claude non si limita a memorizzare tabelle di addizione o a seguire algoritmi tradizionali. Invece, utilizza una combinazione di strategie di approssimazione e calcoli precisi delle cifre che lavorano in parallelo per arrivare alla risposta corretta di 95. Questo approccio suggerisce che le capacità di problem-solving di Claude potrebbero coinvolgere un'elaborazione parallela simile per altri compiti più complessi, utilizzando sia percorsi computazionali approssimativi che precisi che lavorano insieme.